Theory

In order to quantify the information we can extract about certain parameters (position or polarizability of a particle, sample-induced phase shifts,…), we use the concepts of (Quantum) Fisher Information and (Quantum) Cramer Rao Bounds. This allows us to quantitatively compare the sensitivity of different microscopy schemes, and to assess whether these schemes facilitate optimal measurements of a certain parameter for a given specimen. Have you ever wondered whether you should use holography or phase contrast microscopy for label-free live-cell imaging [1]? Or whether it’s better to detect scattering particles in bright- or dark-field [2]?

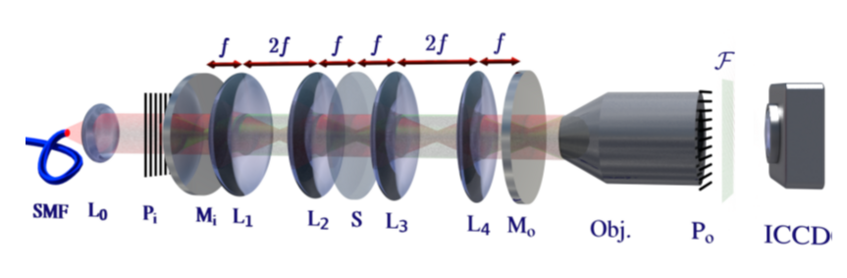
Multi-pass Microscopy

One way to optimize the information obtained per interaction between a probe particle and a sample is to have them interact multiple (m) times. For example, in phase microscopy, the signal-to-noise improves upon multipassing, because the signal scales linearly with m, while the noise stays constant. In dark field microscopy, the signal scales as m squared, while the noise scales as m, again yielding better signal-to-noise. We have shown that this scheme works in light microscopy [3], and are currently investigating whether it could be used to facilitate the optical detection of single proteins.

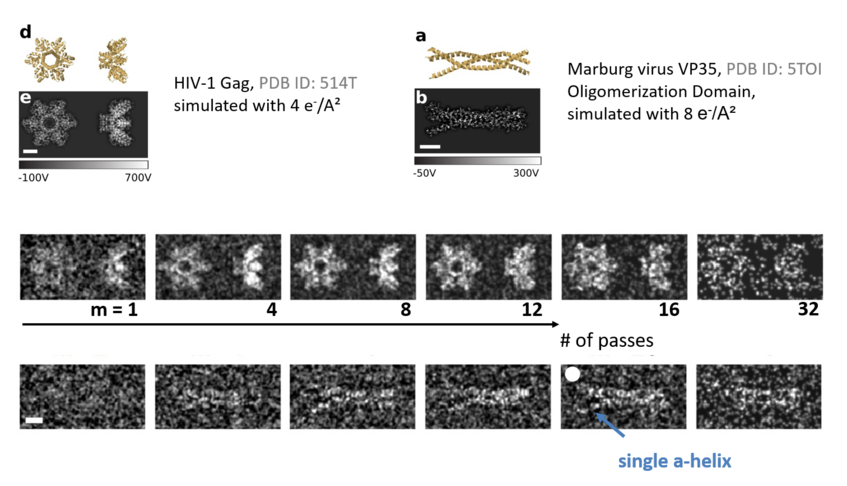
Multipassing could also enhance cryogenic electron microscopy. Images have to be taken at low electron dose to avoid sample damage, such that shot-noise (the statistical fluctuations in the number of detected electrons) limits the achievable spatial resolution. In order to solve the atomic structure of a protein, tens of thousands of images have to be averaged to obtain one image of sufficient signal to noise. While this method had enormous impact on our understanding of biology, it cannot be applied to small proteins, or to proteins that exist in various folding configurations, due to insufficient signal-to-noise. This is a severe limitation given that misfoldings indicate, or cause, several diseases. Cavity and quantum enhanced measurement techniques can alleviate this problem, potentially reducing probe induced sample damage by more than one order of magnitude [4]. A proof-of-concept multi-pass electron microscope is currently under construction [5].

Electron Optics made from Light

Wavefront shaping has enabled numerous exciting possibilities in light optics, ranging from astronomy, to deep-tissue imaging, quantum state engineering [6], to optimized, adaptive phase imaging [7]. In electron optics, wavefront shaping is just beginning to emerge, with applications in aberration correction, exotic-beam creation, or adaptive imaging. We have developed a wavefront shaping device based on the ponderomotive interaction with light [8]. We first shape a light intensity distribution, which then interacts with a counter-propagating electron pulse. The light imparts phase shifts onto the electron beam that are proportional to the local light intensity. In pulsed electron microscopes, this allows for arbitrary electron optics made from light, potentially with thousands of programmable pixels.

Optical Near-Field Electron Microscopy

Finally, we are also working on a hybrid imaging technique where we try to combine the best of two worlds: The spatial resolution of electron optics, and the non-invasiveness of light optics. Our idea is to illuminate a sample with light and then convert the optical near-fields into electrons using a photocathode [9]. The electrons can then be imaged with high spatial resolution. For more information on this European project, please see www.onem.eu.